Gravitation Class 9 Notes Science Chapter 10
This article on ” Gravitation Class 9 Notes Science Chapter 10“ gives you a complete and easy-to-understand summary of this chapter. Whether you’re a CBSE student or from a State Board, these notes will help you revise all the key topics quickly. We’ve explained all important topics such as Centripetal force, Gravitational force, Universal Law of Gravitation, free fall, the difference between mass and weight, thrust, pressure, and buoyancy, Archimedes’ Principle and Relative Density. These notes also include definitions, formulas, differences, diagrams, derivations and examples in a simple language that will help Class 9 students prepare quickly and effectively for exams. Perfect for revision, school tests, and final exams! |
What is Centripetal Force?
- When an object is moving in a circle, it wants to go straight, but something pulls it inward. That inward pull is called centripetal force.
- “Centripetal” means “centre-seeking”.
- It always acts towards the centre of the circle.
- Without a centripetal force, an object cannot stay in circular motion; it would always travel straight line.
So, Centripetal force is the force that keeps a body moving in a circular path by constantly pulling it towards the centre of the circle.
Example:-
- The Earth moves around the Sun due to the centripetal force exerted by the Sun.
- The Moon moves around the Earth due to the centripetal force exerted by the Earth.
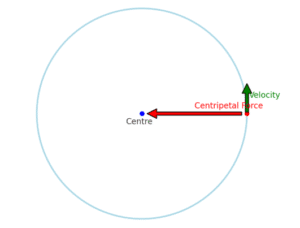
- The red arrow shows the centripetal force pulling the object towards the centre.
- The green arrow shows the direction of the object’s velocity, which is always tangent to the circle.
What is Gravitational Force?
Newton suggested that all objects in the universe attract each other. This force of attraction between objects is called the gravitational force.
So, Gravitational force is the force of attraction between any two objects in the universe.
This force depends on:
- Mass of the objects: It increases if the objects have more mass.
- Distance between them: It decreases if the distance between them is more.
Universal Law of Gravitation by Newton
- The Universal Law of Gravitation states that every object in the universe attracts every other object.
- This force of attraction is called the gravitational force.
- This force is directly proportional to the product of the masses of the two objects.
- This force is inversely proportional to the square of the distance between them (the centers of the two objects).
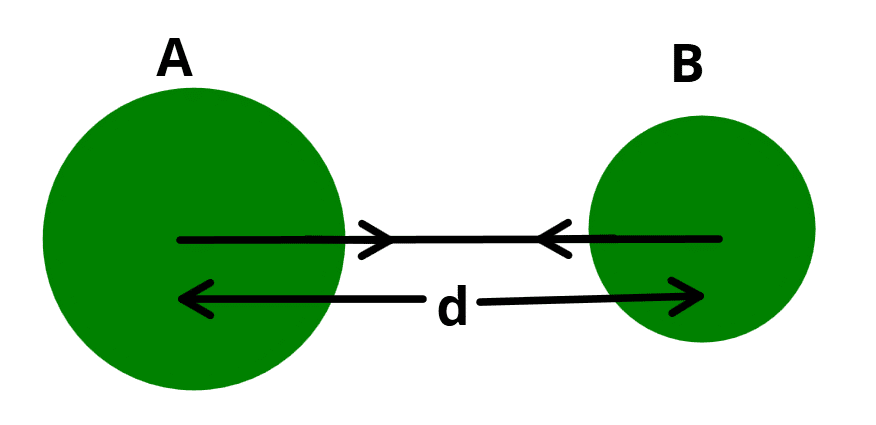
Mathematical representation of Newton’s Universal Law of gravitation
Let two objects A and B of masses m1 and m2 lie at a distance d from each other as shown in the above figure. Let the force of attraction between two objects be F.
\( F\) is directly proportional to to the product of the masses of the two objects: \( F \propto m_1\times m_2\)—————(i)
\( F\) is inversely proportional to the square of the distance: \(F \propto \frac{1}{d^2}\)———(ii)
Combining equations (i), (ii), we get, : \( F \propto \frac{m_1 m_2}{d^2}\)
∴ \( F = G \frac{m_1 m_2}{d^2}\)
where G is the constant of proportionality and is called the universal gravitation constant.
The above equation is the mathematical representation of Newton’s Universal Law of Gravitation
Hence, \( G = F \frac{F d^2}{m_1m_2}\)
The SI unit of G is \( N m^2 kg^2\)
Value of G = 6.673 × 10-11 Nm2 kg-2 (The value was found out by Henry Cavendish.)
Importance of the Universal Law of Gravitation:
The Universal Law of Gravitation is important because it explains how every object in the universe attracts every other object. This law helps us understand many natural phenomena, such as:
- It explains the Earth’s gravitational force
- It helps explain the motion of the Moon around the Earth.
- It explains the motion of the planets around the Sun.
- It explains how tides are caused by the Moon and the Sun.
Free Fall
When an object falls toward the Earth, only under the influence of gravity, it is called free fall. In this case, no other force (like air resistance) is considered.
- When an object is in free fall, its velocity continuously increases, meaning it is accelerating.
- This acceleration is called the acceleration due to gravity and is represented by the letter ‘g’.
- SI Unit of g is m/s².
- The standard value of ‘g’ near the Earth’s surface is approximately 9.8 m/s².
Mathematical Derivation of ‘g’
Newton’s Universal Law of Gravitation states that the force of attraction (F) between between two objects is: \( F = G \frac{M\times m}{d^2}\)
Where,
- F is the gravitational force.
- G is the Universal Gravitational Constant.
- M is the mass of the Earth.
- m is the mass of the object.
- d is the distance between the center of the Earth and the object.
When an object is on or near the Earth’s surface, the distance d is equal to the radius of the Earth, R. So the equation becomes: \( F = G \frac{M\times m}{R^2}\) ———–(i)
We know from Newton’s second law of motion that the force is the product of mass and acceleration: \( F = m\times a\)
But the acceleration due to gravity is represented by the symbol g. Therefore, we can write: \( F = m\times g\)———(ii)
From the equation (i) and (ii), we get: \( m g = G \dfrac{M m}{R^2} \)
or, \( g = G \dfrac{M}{R^2} \)
So, the value of ‘g’ depends on the Universal Gravitational Constant (G), the mass of the Earth (M), and the radius of the Earth (R).
To calculate the value of g
To calculate ‘g’ for the Earth, we need to use the following known values:
- Universal Gravitational Constant (G): 6.7×10−11 N m2 kg-2
- Mass of the Earth (M): 6×1024 kg
- Radius of the Earth (R): 6.4×106 m
We know that, \( g = G \dfrac{M}{R^2} \)
\( g = \frac{6.7 \times 10^{-11} \ \mathrm{N\,m^{2}\,kg^{-2}} \times 6 \times 10^{24} \ \mathrm{kg}}{(6.4 \times 10^{6} \ \mathrm{m})^{2}} \)
\( g = 9.8 ms^{-2}\)
Variation of g on Earth
From the equation \( g = G \dfrac{M}{R^2} \) it is clear that the value of ‘g’ depends upon the distance of the object from the earth’s centre.
So, the value of ‘g’ varies at different parts of the Earth primarily because the Earth is not a perfect sphere.
- The Earth is slightly flattened at the poles and bulges at the equator.
- The radius of the Earth is smaller at the poles than at the equator.
- Since the value of ‘g’ is inversely proportional to the square of the radius, a smaller radius results in a greater value of ‘g’.
- Therefore, the value of ‘g’ is greater at the poles and decreases as we move towards the equator.
- For most calculations, however, ‘g’ is considered to be more or less constant on or near the Earth’s surface.
Motion of Objects under the Influence of Gravitational Force of the Earth:
When an object moves under the influence of the Earth’s gravitational force alone, its motion can be described by the equations of motion. In these equations, the acceleration (‘a’) is replaced by the acceleration due to gravity (‘g’).
The three equations of motion are:
- \(v= u+gt\)
- \( s = ut + \frac{1}{2} gt^2 \)
- \(v^2 = u^2 + 2gs \)
where u and v are the initial and final velocities and s is the distance covered in time, t.
When an object at rest falls towards earth – its initial velocity is zero. So these equations would become as
- \(v= gt\)
- \( s = \frac{1}{2} gt^2 \)
- \(v^2 = 2gs \)
When an object is thrown upwards from the earth – the gravitational force acts in opposite direction, hence g is negative. So these equations would become as
- \(v= u – gt\)
- \( s = ut – \frac{1}{2} gt^2 \)
- \(v^2 = u^2 – 2gs \)
Difference between Mass and Weight
| Mass | Weight |
|---|---|
| Mass is the amount of matter present in a body. | Weight is the force of gravity acting on the body. |
| Mass is the measure of inertia of the body. | Weight is the measure of gravity. |
| The mass of an object is always constant and does not change with location. | The weight of an object can vary at different locations due to a change in the gravitational force. |
| SI Unit is kilograms (kg). | SI Unit is newtons (N). |
| It is a scalar quantity. | It is a vector quantity. |
| It is measured using a beam balance. | It is measured using a spring balance. |
| It stays the same in space or on Earth. | It becomes less in space where gravity is weaker. |
| It can never be zero. | It can be zero at places where there is no gravitational force. |
Weight of an Object on the Moon
The weight of an object is the gravitational force acting on it. The Moon’s mass is much smaller than the Earth’s mass, and its radius is also smaller. Because of this, the Moon’s gravity is weaker than Earth’s gravity.
By applying the Universal Law of Gravitation, it is found that:
\(W_{\text{m}} = \frac{1}{6} \times W_{\text{e}} \)
This means the weight of an object on the moon is one-sixth of its weight on Earth.
Derivation of the Weight of an Object on the Moon
Let:
- \(m \) = mass of the object
- \(M_{\text{e}} \) = mass of the Earth
- \(R_{\text{e}} \) = radius of the Earth
- \(M_{\text{m}} \) = mass of the Moon
- \(R_{\text{m}} \) = radius of the Moon
- \(G \)= universal gravitational constant
By the Universal Law of Gravitation, Weight of an object on the Moon \(W_{\text{m}} \) is:
\(W_{\text{m}} = G \frac{M_{\text{m}} \cdot m}{R_{\text{m}}^2} \)———–(i)
Similarly, Weight of an object on the Earth \(W_{\text{e}} \) is:
\(W_{\text{e}} = G \frac{M_{\text{e}} \cdot m}{R_{\text{e}}^2} \)———–(ii)
To find the relationship between the weight on the Moon and the weight on the Earth, we can divide the two equations:
\( \frac{W_{\text{m}}}{W_{\text{e}}} = \frac{G \frac{M_{\text{m}} \cdot m}{R_{\text{m}}^2}}{G \frac{M_{\text{e}} \cdot m}{R_{\text{e}}^2}} \)
⇒ \( \frac{W_{\text{m}}}{W_{\text{e}}} = \frac{M_{\text{m}} / R_{\text{m}}^2}{M_{\text{e}} / R_{\text{e}}^2} \)
Now Substituting values
\(M_{\text{m}} = 7.36 \times 10^{22} \ \text{kg} \)
\( R_{\text{m}} = 1.74 \times 10^{6} \ \text{m} \)
\( M_{\text{e}} = 5.98 \times 10^{24} \ \text{kg} \)
\( R_{\text{e}} = 6.37 \times 10^{6} \ \text{m} \)
∴ \( \frac{W_{\text{m}}}{W_{\text{e}}} = \frac{ \frac{7.36 \times 10^{22}}{(1.74 \times 10^{6})^2} } { \frac{5.98 \times 10^{24}}{(6.37 \times 10^{6})^2} } \)
∴ \( \frac{W_{\text{m}}}{W_{\text{e}}} = \frac{2.431 \times 10^{10}}{1.474 \times 10^{11}} \approx 0.165 \)
As a fraction,\( 0.165 \) is approximately equal to \( \frac{1}{6} \)
Therefore, we can conclude that:
\( W_{\text{m}} = \frac{1}{6} \times W_{\text{e}} \)
Thrust and Pressure
Thrust
- The force that acts on an object perpendicular to its surface is called thrust.
- It is the net force in a specific direction.
- So, it is a vector quantity.
- The effect of thrust depends on the area on which it acts.
- Example:- The effect of thrust on sand is larger while standing than while lying.
- The SI unit of thrust is N
Pressure
- The force (thrust) that acts per unit area of the object is called pressure.
- Pressure is the thrust per unit area.
- It is calculated by the formula: \( Pressure = \frac{\text{thrust}}{\text{area}} \)
- The SI unit of pressure is pascal (Pa), where:- \(1 \ \text{Pa} = 1 \ \text{N}/\text{m}^2 \)
- The same force acting on a smaller area exerts a larger pressure, and a smaller pressure on a larger area.
Smaller area → higher pressure
Larger area → lower pressure
Buoyancy
- When an object is immersed in a fluid (like water or air), the fluid exerts an upward force on the object.
- This upward force is called the buoyant force or upthrust.
- So, Buoyancy is the upward force exerted by fluids on objects immersed in them.
- The buoyant force acts in the opposite direction of the gravitational force.
- If the upward buoyant force is greater than the weight of the object, the object floats.
- If the buoyant force is smaller than the weight, the object sinks.
- Buoyant force depends on the density of the fluid and the volume of fluid displaced by the object.
Why Objects Float or Sink in Water?
Whether an object floats or sinks in water depends on the relation between its weight and the buoyant force acting on it, and the density of the object compared to water.
When an object is placed in water, two forces act on it:
- Weight of the object: It is the downward force due to gravity.
- Buoyant force:- It is the upward force in the opposite direction of the gravitational force.
Rule of Floating and Sinking
If weight > buoyant force → the object sinks.
If weight < buoyant force → the object floats.
If weight = buoyant force → the object stays partly submerged in water.
Density Concept
The density of a substance is defined as the mass per unit volume.
- If the object’s density is less than the density of the water, the upward buoyant force will be greater than the downward gravitational force. The object will float.
- If the object’s density is greater than the density of the water, the downward gravitational force will be greater than the upward buoyant force. The object will sink.
- If the object’s density is exactly equal to the density of the water, the two forces will be balanced, and the object will remain suspended (neither floating nor sinking).
Examples
- An iron nail sinks because its density is greater than water.
- A cork floats because its density is less than water.
Archimedes’ Principle
Archimedes’ Principle states that when an object is fully or partially immersed in a fluid (a liquid or a gas), it experiences an upward buoyant force. This force is equal to the weight of the fluid that the object pushes aside.
- The upward buoyant force acts in the opposite direction to gravity.
- If the weight of displaced fluid is equal to the weight of the object, then the object floats.
- If the weight of displaced fluid is less than the weight of the object, then the object sinks.
Applications of Archimedes’ Principle
- It is used in designing ships and submarines.
- It is used in lactometers to check the purity of milk.
- It is used in hydrometers to measure the density of liquids.
What is Relative Density?
Relative density is the ratio of the density of a substance to the density of water. Relative density is also called specific gravity.
\( \text{Relative Density} = \frac{\text{Density of the substance}}{\text{Density of water}} \)
Whereas, \( \text{Density} = \frac{\text{Mass}}{\text{Volume}} \)
👉It is a pure number because it has no unit.
Why is Water Chosen as a Reference?
- Water is very common and easily available on Earth.
- Its density is almost constant at normal temperatures ( \( \text{kg/m}^31000 \) at 4°C).
- Because of this, using water as a reference makes calculations easier and comparisons simpler.
How Relative Density Helps to Predict Floating or Sinking?
- If an object has Relative Density less than 1, it means its density is less than that of water. Such objects float in water.
- If an object has Relative Density greater than 1, its density is more than water. Such objects sink in water.
👉 In short:
RD < 1 → Floats
RD > 1 → Sinks
NCERT Notes for Class 9 Science
- Chapter 1 Matter in Our Surroundings Class 9 Notes
- Chapter 2 Is Matter Around Us Pure Class 9 Notes
- Chapter 3 Atoms and Molecules Class 9 Notes
- Chapter 4 Structure of the Atom Class 9 Notes
- Chapter 5 The Fundamental Unit of Life Class 9 Notes
- Chapter 6 Tissues Class 9 Notes
- Chapter 7 Diversity in Living Organisms Class 9 Notes
- Chapter 8 Motion Class 9 Notes
- Chapter 9 Force and Laws of Motion Class 9 Notes
- Chapter 10 Gravitation Class 9 Notes
- Chapter 11 Work, Power And Energy Class 9 Notes
- Chapter 12 Sound Class 9 Notes
- Chapter 13 Why Do we Fall ill Class 9 Notes
- Chapter 14 Natural Resources Class 9 Notes
- Chapter 15 Improvement in Food Resources Class 9 Notes
