NCERT Solutions for Class 9 Science Chapter 9 Force and Laws of Motion

In this article,  you will find NCERT Solutions for Class 9 Science Chapter 9 Force and Laws of Motion. We’ve included all the important numerical problems with step-by-step solutions based on Latest NCERT. Whether you’re studying under CBSE or State Board, these solved examples will help you understand and revise concepts like inertia, momentum, force, Newton’s laws, and more.

These questions are perfect for practice and final exam preparation. Each solution is explained in simple language, so you can learn easily and score better.

NCERT Textbook for Class 9 Science – Page 118

1. Which of the following has more inertia:
(a) a rubber ball and a stone of the same size?
(b) a bicycle and a train?
(c) a five-rupees coin and a one-rupee coin?

Answer:

Inertia depends on mass — the more mass, the more inertia.
(a) A stone of the same size (because it has more mass than a rubber ball)
(b) a train (it has more mass, so much more inertia)
(c) a five-rupees coin (it has more mass, so it has more inertia)

2. In the following example, try to identify the number of times the velocity of the ball changes.
“A football player kicks a football to another player of his team who kicks the football towards the goal The goalkeeper of the opposite team collects the football and kicks it towards a player of his own team”.

Also identify the agent supplying the force in each case.

Answer:

The velocity of football changes four times.

1. When a football player kicks to another player,
2. When that player kicks the football to the goalkeeper.
3. When the goalkeeper stops the football.
4. When the goalkeeper kicks the football towards a player of his own team.

Agent supplying the force:
→ First case – First football player
→ Second case – Second football player
→ Third case – Goalkeeper (hands/legs)
→ Fourth case – Goalkeeper again

3. Explain why some of the leaves may get detached from a tree if we vigorously shake its branch.

Answer:

When we shake a branch of a tree vigorously, some of the leaves may get detached due to the inertia of rest of the leaves. The branch comes into motion and the leaves try to be in the position of rest. Therefore, those leaves that are weak in connection to the branches detach and fall.

 4. Why do you fall in the forward direction when a moving bus brakes to a stop and fall backwards when it accelerates from rest?
Answer:

When a moving bus brakes to a stop:
While a bus is moving, our whole body is also in motion. When the bus stops suddenly due to brakes, the lower portion of our body which are in contact with the bus comes to rest immediately. However, the upper portion continues to move due to the inertia of motion. As a result, we fall in the forward direction.

When the bus accelerates from rest:
When the bus is at rest, our body is also at rest. As the sudden start of the bus brings motion to the bus as well as to our feet in contact with the floor of the bus. But the upper portion tries to stay at rest due to inertia of rest. As a result, we fall in the backward direction.

Class 9 Science NCERT Textbook – Page 126-127

1. If action is always equal to the reaction, explain how a horse can pull a cart?
Answer:

According to Newton’s third law, to every action there is an equal and opposite reaction. So when horse pull the cart, the cart also pull the horse backward with equal force.

But still the horse is able to move forward because it push the ground backward with its feet. In return, the ground exerts an equal and opposite force on the feet of the horse, which enables the horse to move forward. This forward reaction force is greater than the opposing force of cart, so the horse and cart both move ahead.

So the horse move because of the reaction force from ground, not from the cart.

2. Explain, why is it difficult for a fireman to hold a hose, which ejects a large amount of water at a high velocity.
Answer:

When a fireman hold the pipe and water comes out with high speed, the water goes forward with force. According to Newton’s third law, the water also push back the pipe with equal and opposite force.

Because of this reaction force, the pipe try to move backward. It become difficult for the fireman to hold it, specially when water is coming out very fast and in large amount.

So, it is hard to control the pipe due to reaction force of fast moving water.

3. From a rifle of mass 4 kg, a bullet of mass 50 g is fired with an initial velocity of 35 m/s. Calculate the initial recoil velocity of the rifle.
Answer:

Given:

• Mass of bullet, \( m_1 = 50  \text{g} = 0.05  \text{kg} \) \(since ( 1000  \text{g} = 1  \text{kg} )\)

• Mass of rifle, $\text{( m\_2 = 4 text{kg} )}$

• Velocity of bullet, $\text{( v\_1 = 35 text{m/s} )}$

• Recoil velocity of rifle, \( v_2 = ?\)

Initially, the rifle is at rest.
Thus, its initial velocity, \( u = 0\)

Total initial momentum of the rifle and bullet system=\( (m_1+ m_2) u \)= 0

Total momentum of the rifle and bullet system after firing:

\(m_1 v_1 + m_2 v_2 \) = \(0.05\times 35 + 4 v_2 \)

According to the law of conservation of momentum:
Total momentum after the firing = Total momentum before the firing

⇒ \(0.05\times 35 + 4 v_2 \) =0

⇒ \( 1.75 + 4 v_2 \) =0

⇒ \(  4 v_2  = – 1.75 \)

⇒ \(  v_2  = – 0.4375\) m/s

The negative sign shows that the rifle moves in the opposite direction of the bullet.

2. Two objects of masses 100 g and 200 g are moving along the same line and direction with velocities of 2 m/s and 1 m/s respectively.
They collide and after the collision the first object moves at a velocity of 1.67 m./s. Determine the velocity of the second object.

Given:

• Mass of the first object, \(m_1 = 100 g = 0.1 kg \)
• Mass of the second object, \(m_2 = 200 g = 0.2 kg \)
• Initial velocity of the first object, \(u_1  = 2 m/s \)
• Initial velocity of the second object ,\( u_2 = 1 m/s \)
• Final velocity of the first object, \(v_1  = 1.67 m/s \)
• Final velocity of the second object, \( v_2 = ? \)

According to the law of conservation of momentum:
Total momentum before collision = Total momentum after collision

⇒ \(m_1 u_1 + m_2 u_2\)  =\( m_1 v_1 + m_2 v_2\)

⇒ \(( 0.1 )(2) + (0.2 ) (1 )\)  =\( ( 0.1 ) (1.67) + ( 0.2) (v_2)\)

⇒ \( 0.2 + 0.2\)  =\( 0.167 + 0.2 v_2\)

⇒ \( 0.4 \)  =\( 0.167 + 0.2 v_2\)

⇒ \( 0.4 – 0.167\)  =\(   0.2 v_2\)

⇒ \( 0.233\)  =\(   0.2 v_2\)

⇒ \( v_2 = \frac{ 0..233}{ 0.2 } = 1.165 m/s \)

Hence, the velocity of the second object becomes \( 1.165 m/s \) after the collision.

Class 9 Science NCERT Textbook – Page 128

Excercises

1. An object experiences a net zero external unbalanced force. Is it possible for the object to be travelling with a non-zero velocity? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.

Answer

An object can move with non-zero velocity even when no unbalanced force is acting on it. But for this, the object must be moving in constant speed and same direction.

For example, a raindrop falls down with a constant velocity. Because, the gravity pulling it down is balanced by the air resistance pushing it up. So, the net force becomes zero.

So, the conditions are:

1. Its magnitude (speed) must be constant.
2. Its direction must be constant.

2. When a carpet is beaten with a stick, dust comes out of it. Explain.

Answer

When the carpet is beaten with a stick, the carpet moves suddenly, but the dust particles remain at rest due to inertia of rest.

Since the dust doesn’t move with the carpet, it gets separated and  therefore the dust comes out of it.

3. Why is it advised to tie any luggage kept on the roof of a bus with a rope?

Answer

When luggage is kept on the roof of a bus, it is advised to tie it securely with a rope primarily due to the principle of inertia. When a bus suddenly starts, the luggage tends to stay at rest due to inertia of rest and may fall backward. When the bus suddenly stops, the luggage tends to keep moving forward due to inertia of motion and may moving forward. Therefore, it is advised to tie any luggage kept on the roof of a bus with a rope primarily due to the principle of inertia.

4. A batsman hits a cricket ball which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would want to come to rest.

Answer

(c)​ There is a force on the ball opposing the motion.

The ball stops because of friction between the ball and the ground.
Friction is a force that opposes motion, and it gradually slows the ball down until it comes to rest.

5.  A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 metric tonnes (Hint: 1 metric tonne = 1000 kg).

Answer

15. An object of mass 1 kg travelling in a straight line with a velocity of 10 m s⁻¹ collides with, and sticks to, a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the impact. Also, calculate the velocity of the combined object.

Answer

Given that,
Mass of the object, m₁ = 1 kg
Initial velocity of the object before collision, u₁ = 10 m/s
Mass of the wooden block, m₂ = 5 kg
Initial velocity of the wooden block before collision, u₂ = 0 m/s
∴ Total momentum before collision = m₁ u₁ + m₂ u₂
= (1 kg)(10 m/s) + (5 kg)(0 m/s)

= 10 kg⋅m/s + 0 kg⋅m/s

= 10 kg ms⁻¹

It is given that after collision, the object and the wooden block stick together.
Total mass of the combined system = m₁ + m₂
Let their combined velocity be = v
According to the law of conservation of momentum:
Total momentum before collision = Total momentum after collision
m₁ u₁ + m₂ u₂ = (m₁ + m₂)v
⇒ 10 kg ms⁻¹= (1 kg + 5 kg)v

⇒ 10 kg ms⁻¹= (6 kg) v

⇒ \( v = \frac{10 kg. m.s^-1}{6kg} \)

⇒ \( v = \frac{5}{6}m.s^-1 \)
⇒ v  ≈ 1.667 ms⁻¹

Hence, the velocity of the combined object after the collision is approximately 1.667 m/s.

16. An object of mass 100 kg is accelerated uniformly from a velocity of 5 m s⁻¹ to 8 m s-1 in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object.

Answer

Given that,
Mass of the object, m = 100 kg
Initial velocity, u = 5 m/s
Final velocity, v = 8 m/s
Time taken, t = 6 s
∴ Initial momentum = mu = 100 kg × 5 m/s = 500 kg . ms⁻¹
∴ Final momentum = mv = 100 kg × 8 m/s = 800 kg . ms⁻¹

Let the acceleration of the object be, $a$

We know that,

⇒ \( a= \frac{v – u }{t} \)

⇒ \( a= \frac{8 m/s – 5 m/s }{6 s} \)

⇒ \( a= \frac{3 m/s }{6 s} \)

⇒ \( a= o.5 ms^2\)

Now, from Newton’s Second Law of Motion, we have, $F=ma$
∴Force exerted on the object, $F=m\times a$

⇒  F = 100 kg × 0.5 m/s² 

⇒  F = 50 N

Therefore, the magnitude of the force exerted on the object is 50 Newtons.

17. Akhtar, Kiran and Rahul were riding in a motorocar that was moving with a high velocity on an expressway when an insect hit the windshield and got stuck on the windscreen. Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a greater change in momentum as compared to the change in momentum of the motorcar (because the change in the velocity of the insect was much more than that of the motorcar). Akhtar said that since the motorcar was moving with a larger velocity, it exerted a larger force on the insect. And as a result the insect died. Rahul while putting an entirely new explanation said that both the motorcar and the insect experienced the same force and a change in their momentum. Comment on these suggestions.

Answer

Kiran’s suggestion is wrong because the change in momentum is equal for both the insect and the motorcar.

Akhtar is also wrong, as the force exerted by the car and the insect is equal in magnitude.

Rahul’s explanation is correct. Both the car and the insect experience the same force and equal change in momentum. The insect dies not because of a larger force from the car, but because its small mass cannot withstand the immense acceleration caused by that equal force.

18. How much momentum will a dumbbell of mass 10 kg transfer to the floor if it falls from a height of 80 cm? Take its downward acceleration to be 10 m s⁻².

Answer

Mass of the dumbbell, m = 10 kg
Initial velocity of the dumbbell, u = 0 (starts from rest)
Distance covered by the dumbbell, s = 80 cm = 0.8 m
Downward acceleration, a = 10 m/s²
Let, final velocity of the dumbbell (when it was about to hit the floor) = v
We know that:
v² = u² + 2as
⇒ v² = 0 + 2 (10 m/s²) 0.8 m

⇒ v² = 0 + 16 m²/s²

⇒ v² = 16 m²/s²
⇒ v = 4 m/s

Hence, the momentum with which the dumbbell hits the floor is = mv = 10 kg × 4 m/s = 40 kgms⁻¹

∴ The dumbbell will transfer 40 kg⋅m/s of momentum to the floor.

NCERT Textbook for Class 9 Science – Page 130

Additional Excercises

1. The following is the distance-time table of an object in motion:

(a) What conclusion can you draw about the acceleration? Is it constant, increasing, decreasing, or zero?
(b)What do you infer about the forces acting on the object?

Answer

(a) There is an unequal change of distance in an equal interval of time.
Thus, the given object is having a non-uniform motion. Since the velocity of the object is continuously increasing, and therefore acceleration is also increasing over time.  ​Explanation is given below.

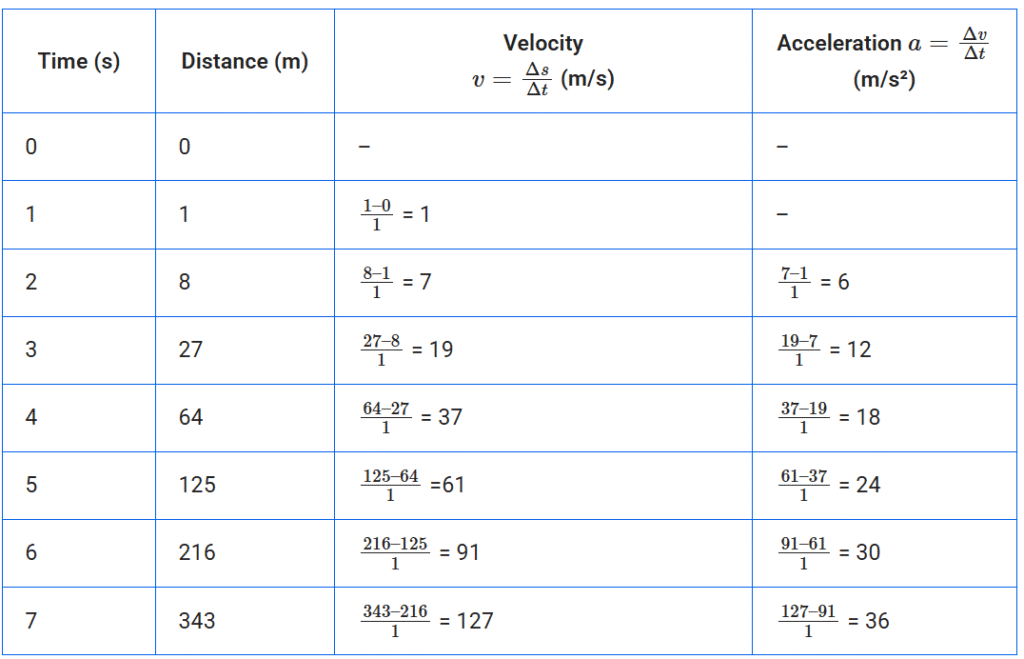
(b)

According to Newton’s Second Law of Motion ($F=ma$), the net force acting on an object is directly proportional to its mass and acceleration.

Since the object’s mass is constant and its acceleration is increasing, it implies that the net force acting on the object must also be increasing over time.

So, we can say unbalanced force is acting on the object.

2. Two persons manage to push a motorcar of mass 1200 kg at a uniform velocity along a level road. The same motorcar can be pushed by three persons to produce an acceleration of 0.2 m s⁻². With what force does each person push the motorcar?
(Assume that all persons push the motorcar with the same muscular effort)

Answer

• Mass of car, m = 1200 kg

• Acceleration, a = 0.2 m/s²

• Number of persons pushing = 3

• Let the force applied by each person F.​

From Newton’s second law of motion:
F= m × a
F = 1200 kg × 0.2 m/s² = 240 N
Thus, the third person applies a force of magnitude 240 N.
Hence, the force with which each person pushes the motorcar is 240 N.

Mass of the hammer, m = 500 g = 0.5 kg
Initial velocity of the hammer, u = 50 m/s
Time taken by the nail to the stop the hammer, t = 0.01 s
Velocity of the hammer, v = 0 (since the hammer finally comes to rest)
From Newton’s second law of motion:
Force,

⇒ \(F = \frac{m(v-u)}{t}\)

⇒ \(F = \frac{0.5 kg(0 – 50 m/s)}{0.01 s}\)

⇒ \(F = \frac{0.5 kg(0 – 50 m/s)}{0.01 s}\)

⇒ \(F = \frac{-25 kg.m/s }{0.01 s}\)

⇒ \(F = -2500 N\)

The hammer strikes the nail with a force of −2500 N. The negative sign indicates that the force acts in the opposite direction to the hammer’s initial motion.

Therefore, the magnitude of the force of the nail on the hammer is 2500 Newtons.

4. A motorcar of mass 1200 kg is moving along a straight line with a uniform velocity of 90 km/h. Its velocity is slowed down to 18 km/h in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.

Answer

Given,
Mass of the motor car, m = 1200 kg

Initial velocity ($u$) = 90 km/h $=90\times \; \backslash (\backslash frac\{5\}\{18\}\backslash )\text{m/s}=5\times 5\text{m/s }=25\text{ m/s}$

Final velocity ($v$) = 18 km/h $=18\times \; \backslash (\backslash frac\{5\}\{18\}\backslash )\text{m/s}=5\text{m/s}$

Time taken, t = 4 s
According to the first equation of motion:
v = u + at

⇒ \( a = \frac{ v – u}{t}\)

⇒ \( a = \frac{5 \text{m/s} – 25 \text{m/s}}{4s}\)

⇒ \( a = \frac{-20\text{m/s}}{4 s}\)

⇒ \( a= -5 \text{m/s}^2\)

Negative sign indicates that its a retarding motion i.e. velocity is decreasing.

We know that change in momentum =

($\Delta p$) = $mv-mu=m(v-u)$

$\Delta p=1200\text{ kg}(5\text{ m/s}-25\text{ m/s})$

$\Delta p=1200\text{ kg}(-20\text{ m/s})$

$\Delta p=-24000\text{ kg}\cdot \text{m/s}$

Therefore, the change in momentum is -24000 kg⋅m/s.

From Newton’s second law of motion:

∵ F = m × a
$\Rightarrow \; F=1200\text{kg }\times (-5\text{m/s2})$

$\Rightarrow \; F=-6000\text{N}$
Hence, the magnitude of the force required is 6000 Newtons. The negative sign indicates that the force is an opposing force, acting to slow the vehicle down.