Force and Laws of Motion : Class 9 Chapter 9 Summary & Notes

What is a Force?

A force is a push or pull that we apply to an object to change its state of motion.

• Force has both direction and magnitude.

• We cannot see a force directly, but we can feel or observe its effects.

• SI unit of force is the newton (N).

A force can:

• Start or stop a moving object.

• Change the speed or direction of motion

• Change the shape or size of an object

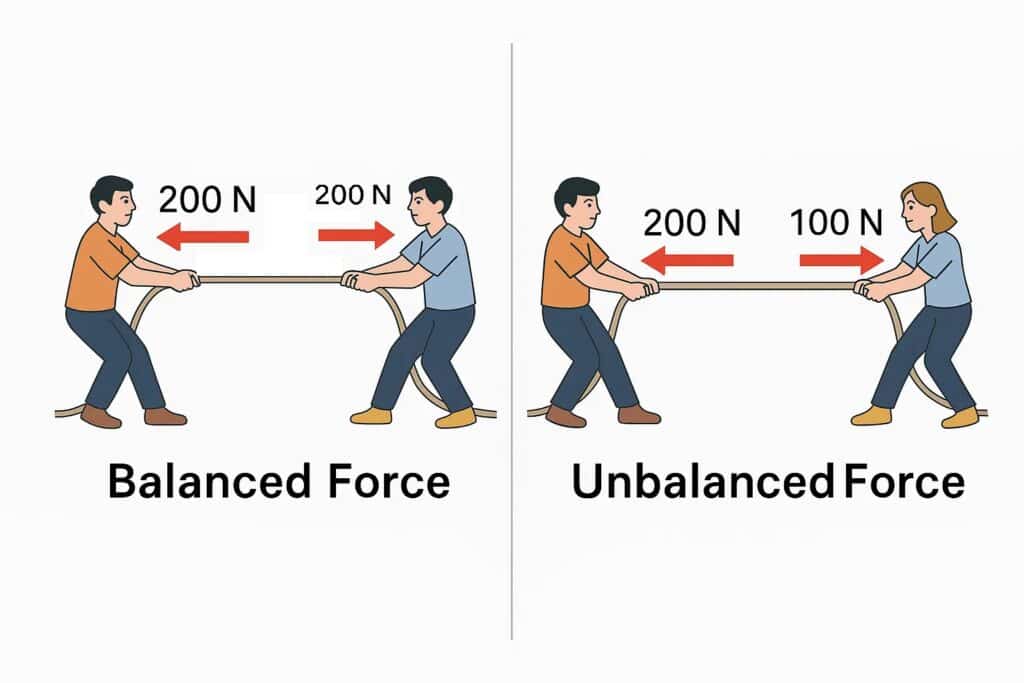
What is Balanced Force?

Balanced forces are two or more forces acting on an object that are equal in magnitude but opposite in direction. They cancel each other out, resulting in no change in the object’s motion.

• A balanced force does not move a stationary object.

• A balanced force does not change the motion of a moving object.

• It may change shape, but not motion.

What is Unbalanced Force?

Unbalanced forces are two or more forces acting on an object that are not equal in magnitude and opposite in direction, or both. They do not cancel each other out, causing the object to move, speed up, slow down, or change direction.

• The object moves in the direction of the stronger force.

• An unbalanced force can start motion, change speed, or change direction.

• It can change the shape and size of an object.

What is the Force of Friction?

Friction arises when two surfaces are in contact with each other. Friction is a force that always acts in the opposite direction of motion. It tries to slow down or stop the moving object.

Examples:

• When you stop pedaling a bicycle, it slows down due to friction.

• You can walk because the friction between your feet and the ground gives grip.

What is the First Law of Motion?

The First Law of Motion is also called the Law of Inertia. It was given by Isaac Newton. It tells us:

An object continues to be in a state of rest or of uniform motion along a straight line unless acted upon by an unbalanced force.

What is Inertia?

Inertia is the tendency of undisturbed objects to stay at rest or to keep moving with the same velocity.

What is Mass?

The mass of an object is a measure of its inertia.

👉 The SI unit of mass  is kilogram (kg)

👉 More mass means more inertia.

👉 Heavier objects are harder to move or harder to stop.

👉 Inertia depends only on mass, not on shape or speed.

Everyday Examples:

• We fall forward when a bus suddenly stops.

• We fall backward when a bus starts moving.

• A pile of carom coins falls straight down if we flick the bottom one — the rest want to stay in place due to inertia.

Inertia of Rest

The inertia of rest is the tendency of an object to remain at rest unless an external force is applied to move it.

Example:

• A coin placed on a card over a glass stays in place when the card is flicked quickly. The coin falls into the glass due to inertia of rest — it resisted motion while the card moved.

Inertia of Motion

The inertia of motion is the tendency of a moving object to keep moving at the same speed in a straight line, unless an external force slows it down or stops it.

Example:

• When a bus suddenly stops, passengers tend to fall forward. Their body wants to keep moving due to the inertia of motion.

Second Law of Motion

In order to understand the Second Law of motion, we need to first understand momentum.

What is Momentum?

Momentum is the product of the mass and velocity of a moving object. Let an object has mass, \( m\) and velocity, \(v \), then its momentum, \(p\) will be

\( p = m\times v \)

• Momentum is a vector quantity, i.e, it has both magnitude and direction.

• The SI unit of momentum is kilogram meter per second (kg·m/s).

• More mass or more speed = more momentum.

• If something is not moving, its momentum is zero.

Examples:

• A moving truck has more momentum than a moving scooter, even at the same speed, because it has more mass.

What is Newton’s Second Law of Motion?

Newton’s Second Law states that:

The rate of change of momentum of an object is directly proportional to the applied unbalanced force, and takes place in the direction of that force.

Mathematical Formulation of the Second Law of Motion:-

Suppose an object of mass, \(m\) is moving along a straight line with an initial velocity, \(u\). It is uniformly accelerated to a final velocity, \(v\) in time, \(t\) by the application of a constant force, \(F\), throughout the time, \(t\).

So,

• Initial momentum, \(p_1\)  =  \(mu\)

• Final momentum,  \(p_2\) = \(mv\)

So, the change in momentum =  \(p_2\) – \(p_1\)

= \(mv\) – \(mu\)

= \( m\times ( v – u ) \)

Now, the rate of change of momentum = \(  \frac{m\times ( v – u )}{t} \)

According to Newton’s 2nd Law, the rate of change of momentum of an object is directly proportional to the applied unbalanced force.

∴ \(F \)∝ \(  \frac{m\times ( v – u )}{t} \)
\(F \) =  \(  k\frac{m\times ( v – u )}{t} \)

\(F \) =  \(  kma\)

Where \( a = \frac{( v – u )}{t} \) is the acceleration.

The quantity, \(k\)  is a constant of proportionality.

For 1 unit of force on 1 kg mass with the acceleration of $1m/{\mathrm{s2}}^{}$, then we have

⇒1 unit of force = \(k\) × (1 kg) × ($m/{\mathrm{s2}}^{}$)

⇒\(k\) = 1.

Therefore, \(F = ma\)

∴ \(Force = mass \times accelaration\)

Deduce the first law of motion from the mathematical expression for the second law of motion.

Or, Proof of Newton’s First Law of Motion from Second Law

From Newton’s 2nd Law of motion, we have

\(F = ma\)

Where:

• \(F \)= aapplied force

• \(m\) = mass of the object

• \(a\) = acceleration

Also, since \( a = \frac{( v – u )}{t} \)​, we can write:

⇒\(F \) =  \(  m(\frac{v – u}{t}) \)

If no external force is applied, then: \(F \)= \(0\)

⇒\( 0 \) =  \(  m(\frac{v – u}{t}) \)

⇒\( 0 \) =  \(  m(v – u) \) [Multiply both sides by \(t\)]

Since mass \( m \neq 0\)

⇒\( 0 \) =  \(  (v – u) \)

⇒\( u \) =  \(  v \)

∴ \(\text{Initial velocity} = \text{Final velocity}\)

Which means, when no force is applied (\(F \)= \(0\)), the object remains at rest or continues moving in a straight line with constant speed.

This is exactly Newton’s First Law of Motion, which states:

“An object remains at rest or in uniform motion unless acted upon by an unbalanced force.”

Newton’s Third Law of Motion 

” To every action, there is an equal and opposite reaction and they act on two different bodies.”

Key Points:

• Both forces are equal in magnitude

• Both forces act in opposite directions

• Both forces act on different objects

• Action and reaction happen at the same time.

• They do not cancel each other because they act on different objects.

Examples:

1. Walking: When you walk, you push the ground backward (action), and the ground pushes you forward with an equal and opposite force (reaction), enabling your movement.
2. Bird flight: A bird pushes air downwards with its wings (action), and the air pushes the bird upwards (reaction), allowing it to fly.
3. Swimming: A swimmer pushes water backward (action), and the water pushes the swimmer forward (reaction).
4. A gun firing a bullet: When a bullet is fired from a gun, the gun exerts a forward force on the bullet (action), and the bullet exerts an equal and opposite backward force on the gun (reaction), causing the gun to recoil.

5. Jumping off a boat: You jump forward, and the boat moves backward.

6. Ball hitting a wall: The ball hits the wall (action), and the wall pushes it back (reaction).

Law of Conservation of Momentum 

The Law of Conservation of Momentum states that the total momentum before an interaction (like a collision) is equal to the total momentum after the interaction, as long as no external force acts on them.

Proof of the Law of Conservation of Momentum

Why Does Momentum Stay Constant?

This law comes from Newton’s Third Law of Motion, which says that for every action, there’s an equal and opposite reaction. When two objects interact (like a hockey stick hitting a ball), the forces they exert on each other are equal in magnitude but opposite in direction. These internal forces cancel out within the system, so the total momentum doesn’t change unless an external force (like friction) gets involved.

For example:

• When a gun fires a bullet, the bullet shoots forward, and the gun recoils backward. The total momentum of the gun and bullet system stays the same.

• If two kids on carts throw a sandbag to each other, the carts move in opposite directions, but the total momentum remains constant.

Deriving the Law of Conservation of Momentum

Let us consider two objects, A and B, with masses \( m_1 \) and \( m_2 \), moving with initial velocities \( u_1 \) and \( u_2 \). Let \( u_1 \) > \( u_2 \) and they collide, and after the collision, their velocities become \( v_1 \) and \( v_2 \). We assume no external forces (like friction) act on the system. During the collision, object A exerts a force \( F_1 \) on object B, and object B exerts a force \( F_2 \) on object A.

Therefore, the total momentum before the collision = \(m_1 u_1 + m_2 u_2\)

And, the total momentum after the collision =\( m_1 v_1 + m_2 v_2\)

For object A, the change in momentum is: \[  m_1 \cdot v_1 – m_1 \cdot u_1 \]

For object B, the change in momentum is: \[  m_2 \cdot v_2 – m_2 \cdot u_2 \]

From Newton’s Second Law, the applied force is the rate of change of momentum. So, during this collision, the force on object A is: \[ F_1=\frac{m_1 \cdot v_1 – m_1 \cdot u_1 }{t} \]

The force on B is : \[ F_2 = \frac{m_2 \cdot v_2 – m_2 \cdot u_2 }{t} \]

From Newton’s third law of motion, object A exerts a force \( F_1 \) on object B, and object B exerts an equal and opposite force \( F_2 \) on object A: \[ F_1 = -F_2 \]

We have: \[ \frac{m_1 \cdot v_1 – m_1 \cdot u_1 }{t} = -\frac{m_2 \cdot v_2 – m_2 \cdot u_2 }{t} \]

⇒ \( m_1 v_1 – m_1 u_1 = -m_2 v_2 + m_2 u_2 \)

⇒ \( m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2 \)

∴ The total momentum before the collision = The total momentum after the collision

This proves the Law of Conservation of Momentum for a system with no external forces.