Class 9 Motion Notes Chapter 8
This article on “Class 9 Motion Notes Chapter 8” gives you a complete and easy-to-understand summary of this chapter. Whether you’re a CBSE student or from a State Board, these notes will help you revise all the key topics quickly. We’ve explained all important topics such as distance, displacement, speed, velocity, acceleration, uniform and non-uniform motion, and graphical representation of motion. Diagrams, examples, derivations and formulas are also included to make your learning fast and effective. These notes also include definitions, formulas, differences, diagrams, derivations and examples in a simple language that will help Class 9 students prepare quickly and effectively for exams. Perfect for revision, school tests, and final exams! See More Class 9 Science Chapter 2: Is Matter Around Us Pure? – Summary, Notes |
Motion
An object is said to be in motion if its position changes with respect to a reference point over time.
Unit: No specific unit.
If something changes its position as time passes, we say it is in motion.
Example:
- A boy walking on the road
A car running on the highway
A plane flying in the sky
Rest
Definition: An object is at rest if its position does not change with respect to a reference point over time.
Example: A book on a table is at rest.
Unit: No specific unit
Reference Point (Origin)
Definition: A fixed point used to describe the position of an object.
Example: A railway station can be a reference point to locate a school.
Unit: No specific unit
Distance
Definition: Distance is the total length of the path covered by an object, irrespective of direction.
Example: If a car travels 5 km, that’s the distance. It is a scalar quantity—only magnitude matters.
Unit: The SI unit of distance is the Metre (m).
Displacement
Definition: Displacement is the shortest distance from the initial to the final position of an object, along with its direction.
Example: If a person moves 3 m east, the displacement is 3 m east. It is a vector quantity.
Unit: The SI unit of distance is the Metre (m) with direction.
Speed
Definition: The distance covered by an object per unit of time.
Formula: \( Speed = \frac{Distance}{Time}\)
Unit: The SI unit of Speed is Metre per second (m/s).
Velocity
Definition: The displacement covered by an object per unit time along a specific direction.
Formula: \(Velocity = \frac{Displacement}{Time}\)
Unit: The SI unit of Velocity is Metre per second (m/s).
Acceleration
Definition: The acceleration of an object is the change in velocity per unit time.
Formula: \(Acceleration = \frac{\text{Change in Velocity}}{\text{Time}}\)
\(Acceleration= \frac{(\text{Final velocity} – \text{Initial velocity})} {Time}\)
\(a= \frac{v – u} {t}\)
Unit: SI Unit of acceleration is m/s² or m s-2 (metres per second squared).
Uniform Motion
Definition: When an object covers equal distances in equal intervals of time in a straight line, it is in uniform motion.
Example: A car moving at a constant speed of 20 m/s.
Unit: No specific unit.
Non-Uniform Motion
Definition: When an object covers unequal distances in equal intervals, it is in non-uniform motion.
Example: A car accelerating or slowing down.
Unit: No specific unit.
Difference Between Uniform and Non-Uniform Motion
| Uniform Motion | Non-Uniform Motion |
|---|---|
| When an object covers equal distances in equal intervals of time. | When an object covers unequal distances in equal intervals of time. |
| Speed remains constant. | Speed keeps changing. |
| Acceleration is zero. | Acceleration is present and may change. |
| A straight slanting line. | A curved line. |
| A car is moving at 60 km/h on a straight road. | A car is moving through city traffic. |
Scalar Quantity
Definition: A physical quantity that has only magnitude (size) and no direction.
Example: distance and speed are scalar quantities.
Unit: Depends on the quantity (e.g., metre for distance, m/s for speed).
Vector Quantity
Definition: A physical quantity that has both magnitude and direction.
Example: displacement, velocity, and acceleration are vector quantities.
Unit: Depends on the quantity (e.g., metre for displacement, m/s for velocity, m/s² for acceleration).
Time
Definition: The duration during which motion or an event occurs. It is used to calculate speed, velocity, or acceleration.
SI Unit: SI Unit of Time is second (s).
Average Speed
Definition: The total distance travelled by an object divided by the total time taken.
Formula: \(Average Speed = \frac{\text{Total Distance}}{Total Time}\)
SI Unit of Average Speed is Metre per second (m/s).
Average Velocity
Definition: The total displacement of an object divided by the total time taken.
Formula: Average Velocity = Total Displacement / Total Time.
Or, \(Average velocity = \frac{\text{initial velocity} + \text{final velocity}}{2}\)
SI Unit of average velocity is Metre per second (m/s) with direction.
Accelerated motion:
Accelerated motion refers to any movement where an object’s velocity (speed and/or direction) changes over time. This change in velocity, whether an increase or decrease in speed, or a change in direction, is known as acceleration.
Uniform Acceleration
Definition: When the velocity of an object changes by an equal amount in equal intervals of time.
Example: A car moving at a constant speed of 5 m every second (5 m/s).
SI Unit of Uniform Acceleration is Metre per second squared (m/s²).
Graphically: Represented by a straight line in a distance-time graph.
Non-uniform Acceleration
Definition: When the velocity of an object changes by an unequal amount in equal intervals of time.
Example: A car moving in traffic (speed changes frequently).
SI Unit: Metre per second squared (m/s²).
Graphically: Represented by a curved or zig-zag line in a distance-time graph.
Positive vs. Negative Acceleration
Positive Acceleration:
- When the velocity of an object increases with time, it is said to have positive acceleration.
- Example:
- A car is increasing its speed from 20 km/h to 50 km/h.
A ball rolling downhill (gravity increases its speed).
Negative Acceleration (Retardation):
- When acceleration is in the opposite direction to velocity, or when the velocity of an object decreases with time, it is said to have negative acceleration. Negative acceleration is also called Retardation and deceleration.
- Example:
A car braking from 30 m/s to 10 m/s.
A ball thrown upward (gravity slows it down).
Uniform Circular Motion
Definition: If an object moves in a circular path with uniform speed, its motion is called uniform circular motion.
Example: The motion of the Moon around the Earth.
Unit: No unit
Equations of Motion
A set of three equations used to describe the motion of an object moving with uniform acceleration along a straight line:
v = u + at
s = ut + ½ at²
v² = u² + 2as
where:
v = final velocity (m/s)
u = initial velocity (m/s)
a = acceleration (m/s²)
t = time (s)
s = displacement (m)
Distance–Time Graph
A distance-time graph shows how the distance travelled by an object changes with time.
Distance is plotted on the y-axis (vertical axis).
Time is plotted on the x-axis (horizontal axis).
- Slope = Change in distance / Change in time = Speed (m/s) (speed = Δs / Δt or v = s2 – s1 / t2 – t1 ).
- The slope (steepness) of the graph represents the speed of the object.
- A steeper slope indicates a higher speed, while a gentler slope indicates a lower speed.
- Straight line: Uniform motion (constant speed).
- Horizontal line: Object at rest (no change in distance).
- Curved line: Non-uniform motion (changing speed).
Different Types of Distance–Time Graphs:
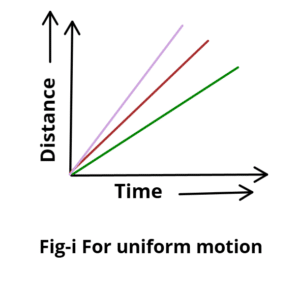
Uniform Motion (Constant Speed)
When an object moves with constant speed, it covers equal distances in equal time intervals.
- The distance travelled by the object is directly proportional to the time taken.
Graph Shape: A straight slanting line.
Key Point:
The slope (steepness) of the line gives the speed of the object.
The greater the slope, the greater the speed.
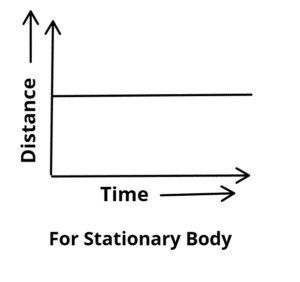
Object at Rest (No Motion)
When an object does not move, the distance remains constant even though time passes.
Graph Shape: A horizontal straight line parallel to the time axis.
- Slope: Zero (speed = 0 m/s).
Non-Uniform Motion (Changing Speed)
When an object moves with a changing speed, it covers unequal distances in equal time intervals.
Graph Shape: A curved line.
- Slope: Varies along the curve. The slope at any point (tangent to the curve) gives the instantaneous speed at that moment.
Key Point:
A curve indicates that speed is not constant (accelerating or decelerating).

Velocity–Time Graphs
A velocity-time graph shows how the velocity of an object changes with time.
Velocity is plotted on the y-axis (vertical axis).
Time is plotted on the x-axis (horizontal axis).
It helps us understand the acceleration, deceleration, and displacement of an object easily.
Different Types of Velocity–Time Graphs:
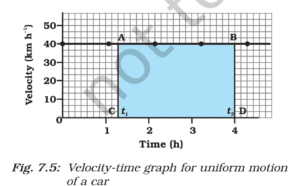
Uniform Velocity (No Acceleration)
When an object moves with constant velocity, meaning no acceleration (a = 0 m/s²).
Graph Shape: A horizontal straight line parallel to the time axis.
- Slope: Zero (acceleration = 0).
- Area under the graph: Displacement = Velocity × Time (rectangular area).
Key Points:
Acceleration = 0
The object moves at constant speed.
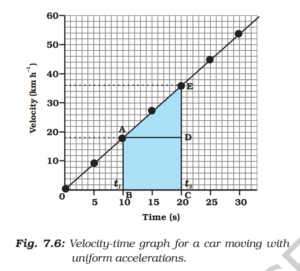
Uniform Acceleration
When an object’s velocity increases uniformly (equal increase in equal time), it shows uniform acceleration.
Graph Shape: A straight slanting line upwards.
Slope: Constant, equal to acceleration (a = Δv / Δt).
- Area under the graph: Displacement = Area of trapezium or triangle (depending on initial velocity).
Key Points:
Constant positive acceleration.
Uniform Deceleration (Negative Acceleration / Retardation)
When an object’s velocity decreases uniformly with time, it shows uniform deceleration.
Graph Shape: A straight slanting line downwards.
- Slope: The graph is a straight slanting line downward, sloping towards the time axis.
- Area under the graph = Area of Triangle Formula: Area=1/2×Base×Height
Key Points:
Constant negative acceleration (retardation).
The slope is constant, showing uniform deceleration.
When the object comes to rest, velocity becomes zero.
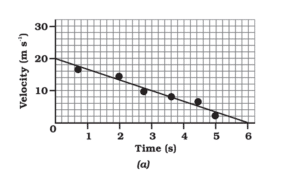
Non-Uniform Acceleration:
- When the velocity changes at a varying rate, indicating non-uniform acceleration.
- Graph: A curved line.
- Slope: Varies along the curve. The slope at any point (tangent to the curve) gives the instantaneous acceleration.
- Area under the graph: Displacement is found by calculating the area under the curve, according to the condition.
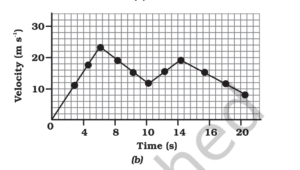
Uniform Circular Motion
When an object moves in a circular path with uniform speed, its motion is called uniform circular motion. (UCM). Even though speed is constant, the direction of velocity is continuously changing, which means the object is accelerating. Hence, UCM is a type of accelerated motion.
Speed \((v) = \frac{2πr}{T}\)
Where:
r = radius of the circle
T = time for one complete revolution (period)
Distinguish between distance and displacement.
| Distance | Displacement |
|---|---|
| The total path length covered by an object during motion. | The shortest distance from the initial position to the final position. |
| It is a Scalar quantity. | It is a vector quantity. |
| It is always positive. | It can be positive, negative, or zero. |
| It depends on the actual path taken. | It depends only on the initial and final positions. |
| Walking 10 m east and 10 m west → Distance = 20 m. | Walking 10 m east and 10 m west → Displacement = 0 m. |
Derive the equation, \(v= u+at\)
Proof:-
Let a body be moving with a uniform acceleration, where
\(u\)= Initial velocity
\(v\) = Final velocity
\(a\) = Uniform acceleration
\(t\)= Time taken
From the definition of Acceleration,
We know:
\(Acceleration = \frac{Change in Velocity}{Time Taken}\)
⇒ \(Acceleration = \frac{Final Velocity-Initial Velocity}{Time Taken}\)
⇒ \(a= \frac{v-u}{t}\)
⇒ \(at= v-u\)
⇒ \(v= u+at\)
Derive the equation, \( s = ut + \frac{1}{2} at^2 \)
Proof:
Let an object be moving with uniform acceleration, a. Let ‘u‘ be the initial velocity and ‘v’ be the final velocity in the time interval ‘t‘. Let ‘s’ be the distance covered by the object during this time interval.
We know,
\(\text{Distance covered = Average velocity × Time taken}\)
Again, we know, \(\text{Average velocity} = \frac{\text{Initial Velocity + Final Velocity}}{2}\)
⇒ \(\text{Distance covered} = \frac{\text{Initial Velocity + Final Velocity}}{2} × \text{Time taken}\)
⇒ \(s = \frac{u + v}{2} × t\)
⇒ \(s = \frac{u + (u + at)}{2} × t\) [Since, \(v= u+at\)]
⇒ \(s = \frac{(2u + at)}{2} × t\)
⇒ \(s = \frac{2ut +at^2}{2} \)
⇒ \(s = ut +\frac{1}{2}at^2 \)
Derive the equation, \(v^2 = u^2 + 2as \)
Proof:-
Let a body be moving with a uniform acceleration, where
\(u\)= Initial velocity
\(v\) = Final velocity
\(a\) = Uniform acceleration
\(t\)= Time taken
- \(s\) = Distance covered
We know, \(s = ut +\frac{1}{2}at^2 \) ——–(i)
and \(v= u+at\)
⇒ \(at = v – u\)
⇒ \(t = \frac{v – u}{a}\) ———-(ii)
Putting this value in equation (i), we have
\(s = u(\frac{v – u}{a}) +\frac{1}{2}a(\frac{v – u}{a})^2 \)
⇒ \(s = (\frac{uv – u^2}{a}) +\frac{1}{2}.a.\frac{1}{a^2}(v^2 – 2uv + u^2)\)
⇒ \(s = (\frac{uv – u^2}{a}) +\frac{(v^2 – 2uv + u^2)}{2a}\)
⇒ \(s = \frac{2(uv -u^2) + (v^2 – 2uv + u^2)}{2a}\)
⇒ \(s = \frac{2uv – 2u^2 + v^2 – 2uv + u^2}{2a}\)
⇒ \(s = \frac{v^2 -u^2}{2a}\)
⇒ \(2as = v^2 -u^2\)
⇒ \(v^2 = u^2 + 2as \)
NCERT Notes for Class 9 Science
- Chapter 1 Matter in Our Surroundings Class 9 Notes
- Chapter 2 Is Matter Around Us Pure Class 9 Notes
- Chapter 3 Atoms and Molecules Class 9 Notes
- Chapter 4 Structure of the Atom Class 9 Notes
- Chapter 5 The Fundamental Unit of Life Class 9 Notes
- Chapter 6 Tissues Class 9 Notes
- Chapter 7 Diversity in Living Organisms Class 9 Notes
- Chapter 8 Motion Class 9 Notes
- Chapter 9 Force and Laws of Motion Class 9 Notes
- Chapter 10 Gravitation Class 9 Notes
- Chapter 11 Work, Power And Energy Class 9 Notes
- Chapter 12 Sound Class 9 Notes
- Chapter 13 Why Do we Fall ill Class 9 Notes
- Chapter 14 Natural Resources Class 9 Notes
- Chapter 15 Improvement in Food Resources Class 9 Notes
